Projects
Chemical Reactions in Solution
To date theoretical treatment of chemical reactions at a fundamental level is only possible for very small systems, not exceeding more than 3-5 atoms. Most chemical reactions of interest occur in the condensed phase, however, in solution, solid/liquid, solid/gaseous interfaces, or in a cellular matrix. If we can accept that our calculations will not be of spectroscopic but at best of chemical accuracy (1-2 kcal/mol), we can introduce two approximations to the full quantum mechanical problem that allow us to describe the chemical dynamics of several hundreds or thousands of particles: Electronic structure calculation with approximate but continuously improving exchange correlation functionals and classical treatment of ionic motion. This is the starting point of state-of-the-art ab initio molecular dynamics simulation programs. Quantum motion of the nuclei can be incorporate for all but the smallest systems using Feynman’s path integral formulation.
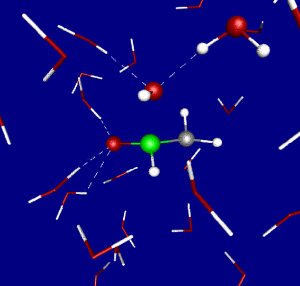
Figure 1: Transition state for the nucleophilic attack of hydroxide on formamide in aqueous solution as obtained from Car-Parrinello molecular dynamics simulation.
While chemical reactions in solution are a subject on its own, they also serve as a reference for enzymatic reactions. Indeed, the catalytic effect of enzymes is usually defined by comparing the rate of the reaction at the active site to the rate of the uncatalyzed reaction in solution. In previous work we have investigated the first step of a reference reaction for peptide bond cleavage in great detail, the nucleophilic attack of hydroxide on formamide HCONH2 + OH– → HC(OH)ONH2– [Angewandte06, CPL06].

Figure 2: Two mechanisms in question: General base mechanism (top panel), and direct nucleophilic attack (bottom panel).
lthough an elementary chemical reaction, the mechanism for alkaline formamide hydrolysis is still controversial, in particular the nature of the attacking species. Kinetic isotope effect measurements suggested a general base mechanism where a water molecule in the first solvation shell of hydroxide is the reactive nucleophile (Fig.2, top panel). More recent kinetic studies favored direct nucleophilic attack of hydroxide (Fig.2, lower panel). Here we aimed to elucidate the detailed mechanism of alkaline formamide hydrolysis using Car-Parrinello metadynamics simulation. We find that hydroxide either accepts a proton transforming one of the water molecules into the reactive hydroxide ion (structural diffusion, path A-D in Fig.3, Fig.4) or attacks the carbonyl bond directly via self diffusion (path E-D in Fig.3). In path A-D hydrogen transfer is completed before the transition state is reached. Hence, we do not find evidence for a general base mechanism proposed recently. The free energy barrier obtained with metadynamics, 22 kcal/mol, is confirmed with an alternative umbrella sampling technique (Fig.3, right panel) and is in excellent agreement with experiment (21.2 kcal/mol). The large free energy barrier in aqueous solution, is related to the breaking of two strong hydrogen bonds formed between the solvent and hydroxide. Such an unfavorable activation process is effectively circumvented in an enzyme active site permitting a rate enhancement by several orders of magnitude. The computed minimum free energy reaction paths depicted in Fig.3 support the interpretation of latest heavy-atom kinetic isotope effect measurements and indicate that the direct nucleophilic attack mechanism is more favourable.

Figure 3, left panel: 2D free energy surface for the first step of formamide hydrolysis obtained from Car-Parrinello metadynamics. rO denotes the distance between the oxygen atom of the attacking species and the C atom of formamide. rH denotes the distance difference between the hydrogen atom and the hydrogen donating and accepting oxygen atom, respectively. A: formamide + hydroxide, B: hydrogen transfer, C: transition state, D: tetrahedral intermediate.

Figure 3, right panel: 1D free energy curve for the direct nucleophilic attack obtained from Car-Parrinello MD combined with umbrella sampling.




Figure 4: Snapshots of molecular configurations along the minimum free energy path A-D shown in Figure 3.
Enzyme catalysis
Nature breaks and forms the strongest chemical bonds with incomparable efficiency using enzymatic catalysis. In living cells enzymes catalyze, for instance, the synthesis of proteins and DNA, the cleavage of carbohydrates and proteins and the transformation of toxic side products of the respiration cycle into harmless compounds. In each case the chemical transformation occurs with high selectivity and at an exceptionally high rate under physiological conditions. The major source of the catalytic power of enzymes is the stabilization of the transition state relative to the reactant and in certain cases and to a smaller extent an increase of tunneling effects. The combined catalytic effects lead to rate enhancements of up to 1019 relative to the uncatalyzed reaction in solution.

Figure 1: Structure of the endoprotease thermolysin. The active site is depicted in stick and ball representation. Thermolysin catalyzes the cleavage of peptide bonds by 5-7 orders of magnitude relative to alkaline hydrolysis in aqueous solution.
With increased capabilities of modern supercomputers force field based molecular dynamics (MD) simulation has advanced to a powerful tool for obtaining detailed insight into the diverse catalytic effects on an ever increasing level of detail. However, the break and formation of chemical bonds requires ab initio based simulation techniques which have serious limitations with regard to system size and time scale. To overcome the problem of the length scale we adopt quantum mechanical/molecular mechanical (QM/MM) simulation methods. In this scheme the active site and substrate molecule is modeled at the quantum level while the protein and solvent is described with an empirical force field. To overcome the time scale problem the QM/MM method is combined with enhanced sampling techniques familiar from classical MD.
Specific aims of my research are:
- The development of techniques that allow for efficient determination of reaction coordinates and free energy profiles of enzymatic reactions at a reasonable accuracy. An example is the combination of the QM/MM method with the recently introduced metadynamics simulation method.
- Improvement of the accuracy of the underlying quantum mechanical calculations, in particular the description of metal-ligand binding energies and distances.
- Detailed investigation of the role of first and second coordination shell and the protein in catalyzing selected enzymatic reactions. Comparison between transition states in an aqueous solvent shell and the one surrounded by the amino acid walls of an active site.
- Aiding the design of biomimetic (artificial) compounds that show novel functions or high catalytic activity.
By studying selected enzymatic systems we aim to draw more general conclusions how enzymes work. The goal is to elucidate the factors that determine activity and selectivity but also the structural features that are not required for the catalytic process. This knowledge can be used, for instance, to help design artificial enzymes that exhibit similar activity as the natural counterparts but have a simpler structure and are therefore cheaper to produce and easier to apply in industrial processes.
A class of enzymes that we are currently studying are Zn2+ containing metalloproteases which are involved in a variety of important biochemical events such as digestion, tissue remodeling and blood pressure regulation. They are also used as models for structure based drug design to be used against tumor invasion and arthritis. Thermolysin which catalyzes peptide bond hydrolysis of large hydrophobic residues is a typical example of this family of proteases (Fig.1). The enzyme is well characterized experimentally but the mechanism of action is still under debate. In order to resolve the controversial mechanistic interpretations of kinetic data we aim to compute reaction free energy profiles for hydrolysis of peptide substrates at the active site using QM/MM molecular dynamics simulation. In current work we have docked a tripeptide to the active center of thermolysin and have computed the free energy barrier for peptide bond cleavage in good agreement with experimental data. Several issues remain to be investigated, however, in particular the effect of different protonation states of active site residues on the reaction mechanism.
Redox free energies and solvation dynamics
Many natural phenomena and technical processes involve the transfer of electrons from donor to acceptor states. When a voltage is applied to the ends of a conducting metal electrons flow until the potential gradient vanishes at each point of the metal. In aerobic cells electrons are transferred from substrate molecules such as carbohydrates to diatomic oxygen after going through a cascade of highly complex enzymatic redox reactions. Iron and zinc surfaces corrode when exposed to air by transferring electrons to oxygen molecules. In fuel cells the (free) energy of chemical compounds is transformed into electric work by electron transfer to the electrode and, reversibly, in electrolysis electric work can be converted to chemical bonding energy (Fig.1, top panel). All these processes have in common that one part of the system donates an electron, i.e. becomes oxidized, and the other accepts an electron, i.e. becomes reduced.
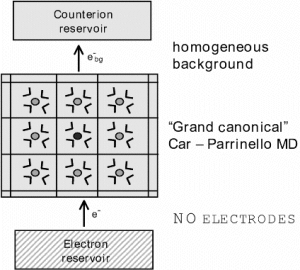
Figure 1: Daniell element (top panel), and model of a half cell reaction amenable to ab initio molecular dynamics simulation (lower panel).
First principle computations of electrochemical quantities such as redox potentials are still in an early stage of development. Such calculations are complicated by the exchange of electrons at the interface of the metallic electrode and the electrolyte. The ab initio simulation of an electrode immersed in an ionic solution such as the Zn or Cu half cell of the Daniell element is still beyond computational capabilities of current supercomputers. In order to avoid the difficulties arising from the metallic/electrolytic 2 phase system we have considered single phase systems so far, in which oxidized and reduced state of a species M remain in solution:
In our approach half cell reactions are modeled by a microscopic cubic box, typically of length 10-15 Angstrom containing one ion and 30-100 solvent molecules (Fig. 1, lower panel). The box is replicated to infinity in each of the three spatial dimensions by applying periodic boundary conditions. The electrode is replaced by an electron reservoir of constant electronic chemical potential μ which allows for the exchange of electrons to and from the system but does not further interact with the ionic solution. In the language of statistical mechanics the model system is called a grand canonical or μVT ensemble, subject to variation of the number of electrons. It should be noted that this model of an electrochemical half cell has some problems. So far the system described is open to electrons, excess (net) charges can be created that lead to an infinite Coulomb energy under periodic boundary conditions and to violation of the principle of electro neutrality. For this reason a homogeneous background charge is introduced which compensates for the excess charge arising from the fluctuation in the number of electrons. In this way the background charge mimics the presence of a counter ion which would be provided by the ionic conductor (clay-diaphragma or salt bridge) in an experiment.

Figure 2: Redox active orbitals of the Cu+aq → Cu2+aq + e- half reaction: highest occupied orbital (HOMO) of aqueous Cu+ (top panel) and lowest unoccupied orbital (LUMO) of aqueous Cu2+. Cu+ is on average coordinated by 4, Cu2+ by 5-6 water molecules. The Cu atom is depicted as a green sphere and water molecules are shown in stick representation.
The link between the microscopic information obtained from molecular simulation and macroscopic quantities such as redox potential is provided by means of statistical mechanics. For the calculation of the redox potential or free energy difference the ensemble of electronic states is restricted to the reduced (R) and oxidized ground states (O) described by two separate potential energy surfaces (PES), ER and EO. At zero electronic chemical potential EO > ER for each ionic configuration. Under equilibrium conditions the two state ensemble is therefore dominated by the reduced state R (Fig. 3, top panel). In order to enforce oxidation we have introduced three independent approaches (Fig. 3, lower panels):
- The grand canonical titration method [PRL02, JACS04 , JCP05] is inspired by the actual electrochemical experiment. Oxidation is enforced by variation of the electronic chemical μ, the computational chemist’s equivalent of the electrode potential. During the dynamics the ion can change its oxidation state depending on how the electronic chemical potential compares to the instantaneous vertical ionization potential. One can rigorously show that the redox potential of the ion is proportional to the particular electronic chemical potential for which the ion is half of the simulation time in the reduced and half of it in the oxidized state. In actual simulations one computes the probability of finding the ion in the oxidized state for several values of μ which produces an S-shaped curve like in a titration (therefore the name). The value of μ at half height of the titration curve is directly related to the redox potential. The advantage of this method is that order parameters are not needed. Sampling problems are rather severe for most applications, however.
- The constrained MD method [JPCB04, JPCB05] makes use of the theory of constraints and enforces oxidation by variation of a suitable order parameter ξ at constant μ. The constrained method allows not only for computation of redox potentials but also also for calculation of non-equilibrium properties such as oxidation free energy barriers along arbitrary geometrical order parameters.
- In the thermodynamic integration method [JCP06] the two potential energy surfaces of R and O are linearly coupled and the system transfered in small steps from R to O by increasing the coupling parameter from 0 to 1. The idea of this method dates back to the thirties but its application in the context of ab initio MD of redox reactions is rather new. Redox potentials and Marcus free energy curves can be computed to good accuracy but the computational cost is usually rather high.

Figure 3: Three ways to enforce a redox reaction. ΔA=AO-AR is the free energy difference between oxidized and reduced states, O and R, described by two potential energy surfaces (PESs) EO and ER, respectively. The free energy difference is related to the redox potential ε by ε=-ΔA/zF, z the number of transferred electrons and F the Faraday constant. μ is the electronic chemical potential, nR the number of electrons in state R, < n > Eμ the expectation value of electrons in the system described by the composite PES Eμ, T the temperature, k the Boltzmann constant, ξ a geometrical order parameter, Hμ the composite Hamiltonian and < IP > Eη the expectation value of the vertical ionization energy averaged over the linearly composed PES Eη.
The free energies computed for the small periodic model cells that can be afforded in ab initio MD can not be related to measurements. This is due to the artificial potential introduced by the homogeneous neutralizing background charge that replaces the counterion. (Note that there is a classical correction formula for this artifact; we find, however, that it does not apply to our DFT (GGA) electronic structure calculation.) The free energies of half reactions have therefore no meaning. However, free energies of full redox reactions, obtained as differences of half reactions , can be compared to experiment, but only if the reactant (and product) species of the two half reactions have the same charge. Under these conditions long range interactions cancel to a good approximation and the redox potential is mainly determined by short range or “chemical” interactions between solute and solvent. The practical justification we can offer here is the success of our scheme in reproducing a number of experimental redox potentials for full reactions (computed as differences of half reactions) of aqueous transition metal complexes (Figs. 2 and 4) and organic molecules. The error wrt experiment is typically 0.1-0.2 eV.




Figure 4: Redox active orbitals for the Ag+aq → Ag2+aq + e- and Ru2+aq → Ru3+aq + e- half reactions in aqueous solution. From left to right: HOMO of Ag+, LUMO of Ag2+, HOMO of Ru2+, LUMO of Ru3+. The average water coordination numbers of these ions are 4, 5-6, 6 and 6. The Ag atom is depicted as a red sphere and the Ru atom as a blue sphere. Water molecules are shown in stick representation.

